Cohort discrete time state transition model

Source: R/dtstm.R

Simulate outcomes from a cohort discrete time state transition model.

Format

An R6::R6Class object.

References

Incerti and Jansen (2021). See Section 2.1 for a description of a cohort DTSTM and details on simulating costs and QALYs from state probabilities. An example in oncology is provided in Section 4.3.

See also

CohortDtstm objects can be created from model objects as documented in create_CohortDtstm(). The CohortDtstmTrans documentation describes the class for the transition model and the StateVals documentation describes the class for the cost and utility models. A CohortDtstmTrans object is typically created using create_CohortDtstmTrans().

There are currently three relevant vignettes. vignette("markov-cohort") details a relatively simple Markov model and vignette("markov-inhomogeneous-cohort") describes a more complex time inhomogeneous model in which transition probabilities vary in every model cycle. The vignette("mlogit") shows how a transition model can be parameterized using a multinomial logistic regression model when transition data is collected at evenly spaced intervals.

Public fields

trans_model

The model for health state transitions. Must be an object of class CohortDtstmTrans.

utility_model

The model for health state utility. Must be an object of class StateVals.

cost_models

The models used to predict costs by health state. Must be a list of objects of class StateVals, where each element of the list represents a different cost category.

stateprobs_

An object of class stateprobs simulated using $sim_stateprobs().

qalys_

An object of class qalys simulated using $sim_qalys().

costs_

An object of class costs simulated using $sim_costs().

Methods

Public methods

Method new()

Create a new CohortDtstm object.

Usage

CohortDtstm$new(trans_model = NULL, utility_model = NULL, cost_models = NULL)

Arguments

trans_model

The trans_model field.

utility_model

The utility_model field.

cost_models

The cost_models field.

Returns

A new CohortDtstm object.

Method sim_stateprobs()

Simulate health state probabilities using CohortDtstmTrans$sim_stateprobs().

Usage

CohortDtstm$sim_stateprobs(n_cycles)

Arguments

n_cycles

The number of model cycles to simulate the model for.

Returns

An instance of self with simulated output of class stateprobs stored in stateprobs_.

Method sim_qalys()

Simulate quality-adjusted life-years (QALYs) as a function of stateprobs_ and utility_model. See sim_qalys() for details.

Usage

CohortDtstm$sim_qalys(
  dr = 0.03,
  integrate_method = c("trapz", "riemann_left", "riemann_right"),
  lys = TRUE
)

Arguments

dr

Discount rate.

integrate_method

Method used to integrate state values when computing costs or QALYs. Options are trapz for the trapezoid rule, riemann_left for a left Riemann sum, and riemann_right for a right Riemann sum.

lys

If TRUE, then life-years are simulated in addition to QALYs.

Returns

An instance of self with simulated output of class qalys stored in qalys_.

Method sim_costs()

Simulate costs as a function of stateprobs_ and cost_models. See sim_costs() for details.

Usage

CohortDtstm$sim_costs(
  dr = 0.03,
  integrate_method = c("trapz", "riemann_left", "riemann_right")
)

Arguments

dr

Discount rate.

integrate_method

Method used to integrate state values when computing costs or QALYs. Options are trapz for the trapezoid rule, riemann_left for a left Riemann sum, and riemann_right for a right Riemann sum.

Returns

An instance of self with simulated output of class costs stored in costs_.

Method summarize()

Summarize costs and QALYs so that cost-effectiveness analysis can be performed. See summarize_ce().

Usage

CohortDtstm$summarize(by_grp = FALSE)

Arguments

by_grp

If TRUE, then costs and QALYs are computed by subgroup. If FALSE, then costs and QALYs are aggregated across all patients (and subgroups).

Method clone()

The objects of this class are cloneable with this method.

Usage

CohortDtstm$clone(deep = FALSE)

Arguments

deep

Whether to make a deep clone.

Examples

library("data.table")
library("ggplot2")
theme_set(theme_bw())
set.seed(102)

# NOTE: This example replicates the "Simple Markov cohort model" 
# vignette using a different approach. Here, we explicitly construct
# the transition probabilities "by hand". In the vignette, the transition 
# probabilities are defined using expressions (i.e., by using 
# `define_model()`). The `define_model()` approach does (more or less) what 
# is done here under the hood.

# (0) Model setup
hesim_dat <- hesim_data(
  strategies = data.table(
    strategy_id = 1:2,
    strategy_name = c("Monotherapy", "Combination therapy")
  ),
  patients <- data.table(patient_id = 1),
  states = data.table(
    state_id = 1:3,
    state_name = c("State A", "State B", "State C")
  )
)
n_states <- nrow(hesim_dat$states) + 1
labs <- get_labels(hesim_dat)

# (1) Parameters
n_samples <- 10 # Number of samples for PSA

## Transition matrix
### Input data (one transition matrix for each parameter sample,
###             treatment strategy, patient, and time interval)
p_id <- tpmatrix_id(expand(hesim_dat, times = c(0, 2)), n_samples)
N <- nrow(p_id)

### Transition matrices (one for each row in p_id)
p <- array(NA, dim = c(n_states, n_states, nrow(p_id)))

#### Baseline risk
trans_mono <- rbind(
  c(1251, 350, 116, 17),
  c(0, 731, 512, 15),
  c(0, 0, 1312, 437),
  c(0, 0, 0, 469)
)
mono_ind <- which(p_id$strategy_id == 1 | p_id$time_id == 2)
p[,, mono_ind] <- rdirichlet_mat(n = 2, trans_mono)

#### Apply relative risks
combo_ind <- setdiff(1:nrow(p_id), mono_ind)
lrr_se <- (log(.710) - log(.365))/(2 * qnorm(.975))
rr <- rlnorm(n_samples, meanlog = log(.509), sdlog = lrr_se)
rr_indices <- list( # Indices of transition matrix to apply RR to
  c(1, 2), c(1, 3), c(1, 4),
  c(2, 3), c(2, 4),
  c(3, 4)
)
rr_mat <- matrix(rr, nrow = n_samples, ncol = length(rr_indices))
p[,, combo_ind] <- apply_rr(p[, , mono_ind],
                            rr = rr_mat,
                            index = rr_indices)
tp <- tparams_transprobs(p, p_id)

## Utility
utility_tbl <- stateval_tbl(
  data.table(
    state_id = 1:3,
    est = c(1, 1, 1)
  ),
  dist = "fixed"
)

## Costs
drugcost_tbl <- stateval_tbl(
  data.table(
    strategy_id = c(1, 1, 2, 2),
    time_start = c(0, 2, 0, 2),
    est = c(2278, 2278, 2278 + 2086.50, 2278)
  ),
  dist = "fixed"
)

dmedcost_tbl <- stateval_tbl(
  data.table(
    state_id = 1:3,
    mean = c(A = 1701, B = 1774, C = 6948),
    se = c(A = 1701, B = 1774, C = 6948)
  ),
  dist = "gamma"
)

cmedcost_tbl <- stateval_tbl(
  data.table(
    state_id = 1:3,
    mean = c(A = 1055, B = 1278, C = 2059),
    se = c(A = 1055, B = 1278, C = 2059)
  ),
  dist = "gamma"
)

# (2) Simulation
## Constructing the economic model
### Transition probabilities
transmod <- CohortDtstmTrans$new(params = tp)

### Utility
utilitymod <- create_StateVals(utility_tbl,
                               hesim_data = hesim_dat,
                               n = n_samples)

### Costs
drugcostmod <- create_StateVals(drugcost_tbl,
                                hesim_data = hesim_dat,
                                n = n_samples)
dmedcostmod <- create_StateVals(dmedcost_tbl,
                                hesim_data = hesim_dat,
                                n = n_samples)
cmedcostmod <- create_StateVals(cmedcost_tbl,
                                hesim_data = hesim_dat,
                                n = n_samples)
costmods <- list(drug = drugcostmod,
                 direct_medical = dmedcostmod,
                 community_medical = cmedcostmod)

### Economic model
econmod <- CohortDtstm$new(trans_model = transmod,
                           utility_model = utilitymod,
                           cost_models = costmods)

## Simulating outcomes
econmod$sim_stateprobs(n_cycles = 20)
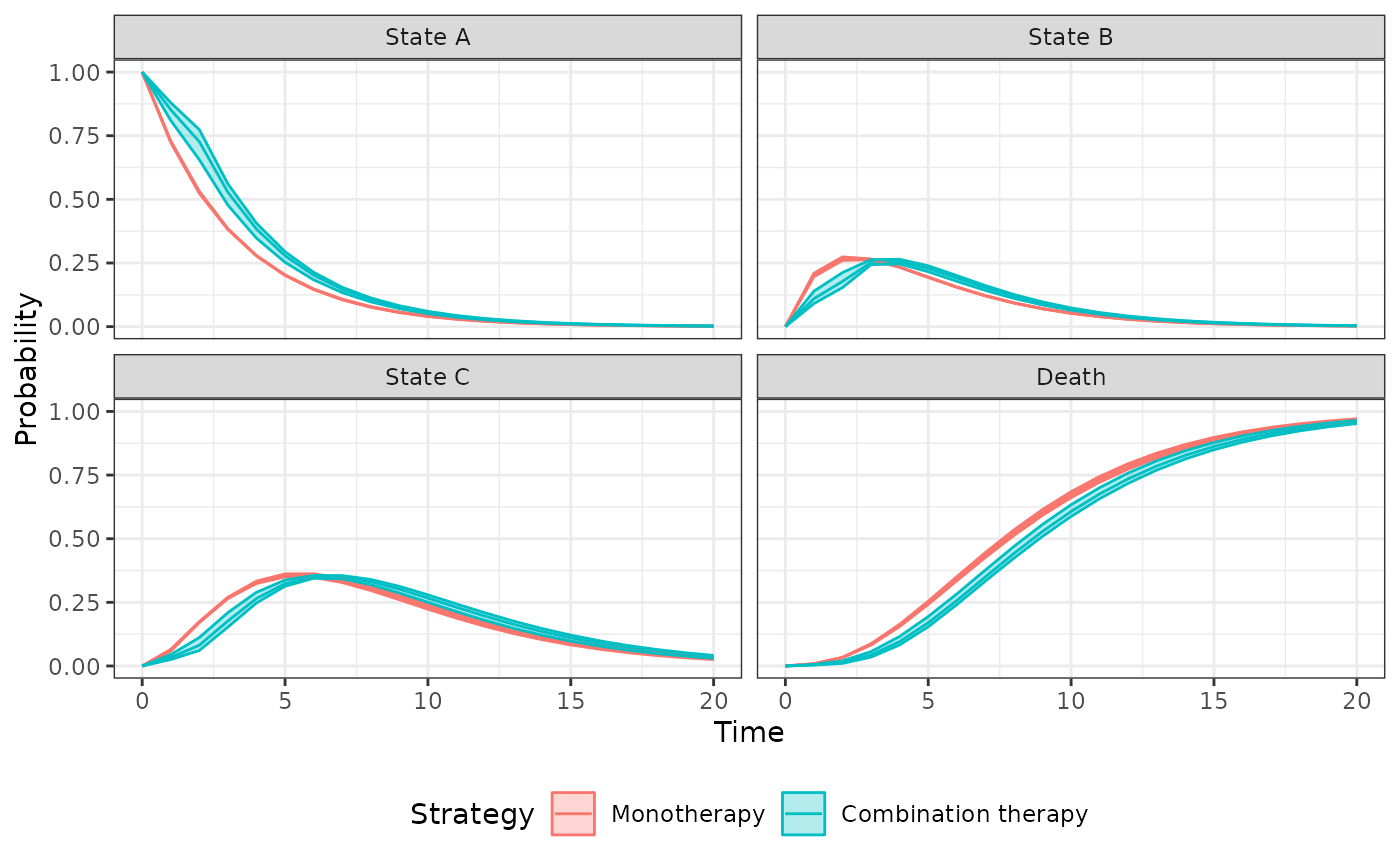
autoplot(econmod$stateprobs_, ci = TRUE, ci_style = "ribbon",
         labels = labs)

econmod$sim_qalys(dr = 0, integrate_method = "riemann_right")
econmod$sim_costs(dr = 0.06, integrate_method = "riemann_right")

# (3) Decision analysis
ce_sim <- econmod$summarize()
wtp <- seq(0, 25000, 500)
cea_pw_out <- cea_pw(ce_sim, comparator = 1, dr_qalys = 0, dr_costs = .06,
                     k = wtp)
format(icer(cea_pw_out))
#>              Outcome                       2
#>               <fctr>                  <char>
#> 1: Incremental QALYs       0.88 (0.42, 1.26)
#> 2: Incremental costs      5,252 (401, 8,617)
#> 3:   Incremental NMB 38,957 (17,712, 56,120)
#> 4:              ICER                   5,940