Partitioned survival models

2024-09-18

Source: vignettes/psm.Rmd

Overview

An N-state partitioned survival model (PSM) simulates the probability that a patient is in each of N distinct health states at a given point of time when treated by a particular therapy. State membership is estimated from a set of non-mutually exclusive survival curves; for an N-state model, N-1 survival curves are required.

The cumulative survival function, Sn(t)S_n(t), represents the probability that a patient survives to health state nn or to a lower indexed state beyond time tt. The probability that a patient is in health state 1 is always just S1(t)S_1(t). State membership in health states 2,…,n−12,\ldots, n-1 is calculated as Sn(t)−Sn−1(t)S_{n}(t) - S_{n-1}(t). Finally, the probability of being in the final health state NN (i.e., the dead state) is 1−SN−1(t)1-S_{N-1}(t), or one minus the overall survival curve.

In hesim, an N-state PSM consists of three types of separate statistical models: a set of N-1 survival models, a model of the utility values to assign to each health state, and a set of models for costs to assign to each health state. Multiple cost models can be used to categorize costs into different categories (e.g., costs of medical care, drug costs). All models can either be fit using R or constructed with external data.

Separate survival curves as a function of time, tt, are predicted for each treatment strategy kk and patient ii as a function of LL parameters, αl\alpha_l, which can depend on covariates, xlx_l (see params_surv() for more details),

Sn(t|α1n(x1n,ik),…,αLn(xLn,ik)). \begin{aligned} S_{n}(t|\alpha_{1n}(x_{1n, ik}), \ldots, \alpha_{Ln}(x_{Ln, ik})). \end{aligned} Quality-adjusted life-years (QALYs) and total costs associated with a given health state for a given treatment strategy and patient are calculated by integrating the “weighted” probability of survival, where weights are a function of the discount factor and predicted state values. Letting hh index a health state, QALYs and total costs for the mmth cost category are calculated as,

$$ \begin{aligned} \rm{QALYs}_{hik} &= \int_{0}^{T} q_{hik}(t) e^{-rt} p_{hik}(t)dt, \\ \rm{Costs}_{m,hik} &= \int_{0}^{T} c_{m,hik}(t) e^{-rt} p_{hik}(t)dt, \end{aligned} $$ where qhikq_{hik} is a quality-of-life weight, cm,hikc_{m,hik} is (assuming that time is measured in years) annualized costs, rr is the discount rate, and phik(t)p_{hik}(t) is the probability of being in a given health state at a given time, and QALYs and costs are calculated over TT time periods.

An example 4-state PSM

To illustrate a partitioned survival analysis, consider the evaluation of a two-line sequential treatment strategy in oncology using a 4-state PSM. The 4 health states might be:

  • Progression free on first line treatment
  • Progression free on second line treatment
  • Progressed on second line treatment
  • Death

We begin by defining the population, treatment strategies, and model structure. In this example, we model three treatment strategies, three distinct patients (that differ in age and gender), and four health states (death and three non-death states). This information is combined using hesim_data(), which creates a general object of class hesim_data.

library("data.table")
library("hesim")
set.seed(101)
strategies <- data.table(strategy_id = c(1, 2, 3),
                         strategy_name = paste0("Strategy ", 1:3))
patients <- data.table(patient_id = seq(1, 3),
                       age = c(45, 50, 60),
                       female = c(0, 0, 1))
states <- data.frame(state_id =  seq(1, 3),
                     state_name = c("Progression free (1st line)",
                                    "Progression free (2nd line)",
                                    "Progressed (2nd line)"),
                        stringsAsFactors = FALSE)
hesim_dat <- hesim_data(strategies = strategies,
                        patients = patients,
                        states = states)
print(hesim_dat)
## $strategies
##    strategy_id strategy_name
##          <num>        <char>
## 1:           1    Strategy 1
## 2:           2    Strategy 2
## 3:           3    Strategy 3
## 
## $patients
##    patient_id   age female
##         <int> <num>  <num>
## 1:          1    45      0
## 2:          2    50      0
## 3:          3    60      1
## 
## $states
##   state_id                  state_name
## 1        1 Progression free (1st line)
## 2        2 Progression free (2nd line)
## 3        3       Progressed (2nd line)
## 
## attr(,"class")
## [1] "hesim_data"

We use get_labels() to obtain nice labels for plots and summary tables.

labs <- get_labels(hesim_dat)
print(labs)
## $strategy_id
## Strategy 1 Strategy 2 Strategy 3 
##          1          2          3 
## 
## $state_id
## Progression free (1st line) Progression free (2nd line) 
##                           1                           2 
##       Progressed (2nd line)                       Death 
##                           3                           4

Parameter estimation

Survival models

The parameters of the survival models would typically be estimated in one of two ways. First, if access to patient level data from a clinical trial were available, survival models would be fit using available R packages. Second, a formal evidence synthesis—such as a network meta-analysis—might be conducted. Here, we provide an example of an analysis with trial level data.

We consider an estimation dataset (surv_est_data) with three survival endpoints with endpoint 1 denoting the lowest indexed state, endpoint 2 the next indexed state, and endpoint 3 representing overall survival. In our example, endpoint 1 represents progression on 1st line treatment, endpoint 2 represents progression on 2nd line treatment, and endpoint 3 represents death.

Survival models in hesim can be fit using either flexsurvreg or flexsurvspline from the flexsurv package. hesim currently supports parametric (exponential, Weibull, Gompertz, gamma, log-logistic, lognormal, and generalized gamma), splines, and fractional polynomial survival models (see params_surv). In this example, we fit a Weibull model to each of the three survival endpoints.

library("flexsurv")
surv_est_data <- psm4_exdata$survival
fit1 <- flexsurvreg(Surv(endpoint1_time, endpoint1_status) ~ age + female + 
                    factor(strategy_id),
                    data = surv_est_data,
                    dist = "weibull")
fit2 <- flexsurvreg(Surv(endpoint2_time, endpoint2_status) ~ age + female +
                    factor(strategy_id),
                    data = surv_est_data,
                    dist = "weibull")
fit3 <- flexsurvreg(Surv(endpoint3_time, endpoint3_status) ~ age + female +
                    factor(strategy_id),
                    data = surv_est_data,
                    dist = "weibull")
psfit_wei <- flexsurvreg_list(fit1, fit2, fit3)

Utility and cost models

Although utility and cost models can be fit using regression models, in many cases, we won’t fit a model directly, but will use estimated mean values from published sources. In this case, we can use a stateval_tbl() to store estimates. For instance, consider an example where we are only given a range of values for utility and we therefore approximate the posterior distribution of mean utility values by health state using a uniform distribution.

utility_tbl <- stateval_tbl(tbl = data.frame(state_id = states$state_id,
                                             min = psm4_exdata$utility$lower,
                                             max = psm4_exdata$utility$upper),
                            dist = "unif")

Similar to utility, we will not simulate drug costs based on a statistical model but will instead use published estimates. Drug costs will only vary by treatment strategy (i.e., they do not vary by health state or across samples in the PSA).

drugcost_tbl <- stateval_tbl(tbl = data.frame(strategy_id = strategies$strategy_id,
                                           est = psm4_exdata$costs$drugs$costs),
                          dist = "fixed")

For cases in which we want to use a regression model to simulate costs, hesim supports parameterizing a cost or utility model using linear models. Here, we fit a model for medical costs as a function of the three non-death health states using the lm() function in R.

medcosts_fit <- lm(costs ~ female + state_name, data = psm4_exdata$costs$medical)

Simulation

Constructing the economic model

A PSM in hesim is an R6 object of class Psm and comprises of three separate submodels: (1) a set of survival models for generating survival curves (of class PsmCurves), (2) a utility model (of class StateVals), and (3) a set of cost models for each cost component (a list of StateVals objects). Since analyses in hesim are, by default, based on sampled values of the parameters from their joint posterior distribution in order to facilitate probabilistic sensitivity analysis (PSA), we will specify the number of sampled parameter sets that are desired.

n_samples <- 100

Survival models

Survival curves are simulated using PsmCurves objects. We can create a PsmCurves object using create_PsmCurves() as a function of our fitted Weibull models and input data describing the target population and treatment strategies.

To conduct the PSA, we must sample random draws of the regression coefficients from suitable probability distribution, which can be done in one of two ways. First, the parameters of each survival model can be sampled separately using a multivariate normal distribution. However, this option does not preserve the correlation in the survival endpoints. By default, create_PsmCurves() consequently samples the parameters via bootstrapping, whereby the survival models are refit repeatedly to resamples of the estimation dataset.

surv_input_data <- expand(hesim_dat, by = c("strategies", "patients"))
survmods <- create_PsmCurves(psfit_wei, input_data = surv_input_data, n = n_samples,
                               uncertainty = "bootstrap", est_data = surv_est_data)

Utility and cost models

Utility and cost values are simulated using models of class StateVals. We can instantiate a StateVals object from a ’stateval_tbl` object, which creates a “mean model” that predicts mean state values for each treatment strategy, patient, and health state combination. In the utility model, utility only varies across health states and is constant within patients and treatment strategies conditional on health state.

utilitymod <- create_StateVals(utility_tbl, n = n_samples, hesim_data = hesim_dat)

We take a similar approach for drug costs, in which costs only vary across treatment strategies.

drugcostmod <- create_StateVals(drugcost_tbl, n = n_samples, hesim_data = hesim_dat)

Finally, we can also instantiate a StateVals() from a fitted linear model and a corresponding dataset of class expanded_hesim_data.

medcost_data <- expand(hesim_dat, by = c("strategies", "patients", "states"))
medcostmod <- create_StateVals(medcosts_fit, input_data = medcost_data, 
                                 n = n_samples)

Combining the statistical models

The PSM model is instantiated using $new().

psm <- Psm$new(survival_models = survmods,
               utility_model = utilitymod,
               cost_models = list(medical = medcostmod, 
                                  drug = drugcostmod))

Simulating outcomes

Simulating survival curves

Survival curves are predicted by treatment strategy and patient with the function $sim_survival(). We can quickly generate a plot of survival curves (averaged across patients) by treatment strategy using autoplot.survival().

# Simulate
times <- seq(0, 12, by = .1)
psm$sim_survival(t = times)
head(psm$survival_)
##    sample strategy_id patient_id grp_id curve     t  survival
##     <num>       <int>      <int>  <int> <num> <num>     <num>
## 1:      1           1          1      1     1   0.0 1.0000000
## 2:      1           1          1      1     1   0.1 0.9189061
## 3:      1           1          1      1     1   0.2 0.8411512
## 4:      1           1          1      1     1   0.3 0.7688137
## 5:      1           1          1      1     1   0.4 0.7019982
## 6:      1           1          1      1     1   0.5 0.6405107
# Plot
library("ggplot2")
labs$curve <- c("Curve 1" = 1, "Curve 2" = 2, "Curve 3" = 3)
autoplot(psm$survival_, labels = labs,
         ci = TRUE, ci_style = "ribbon") +
  scale_x_continuous(breaks = seq(0, max(times), 2))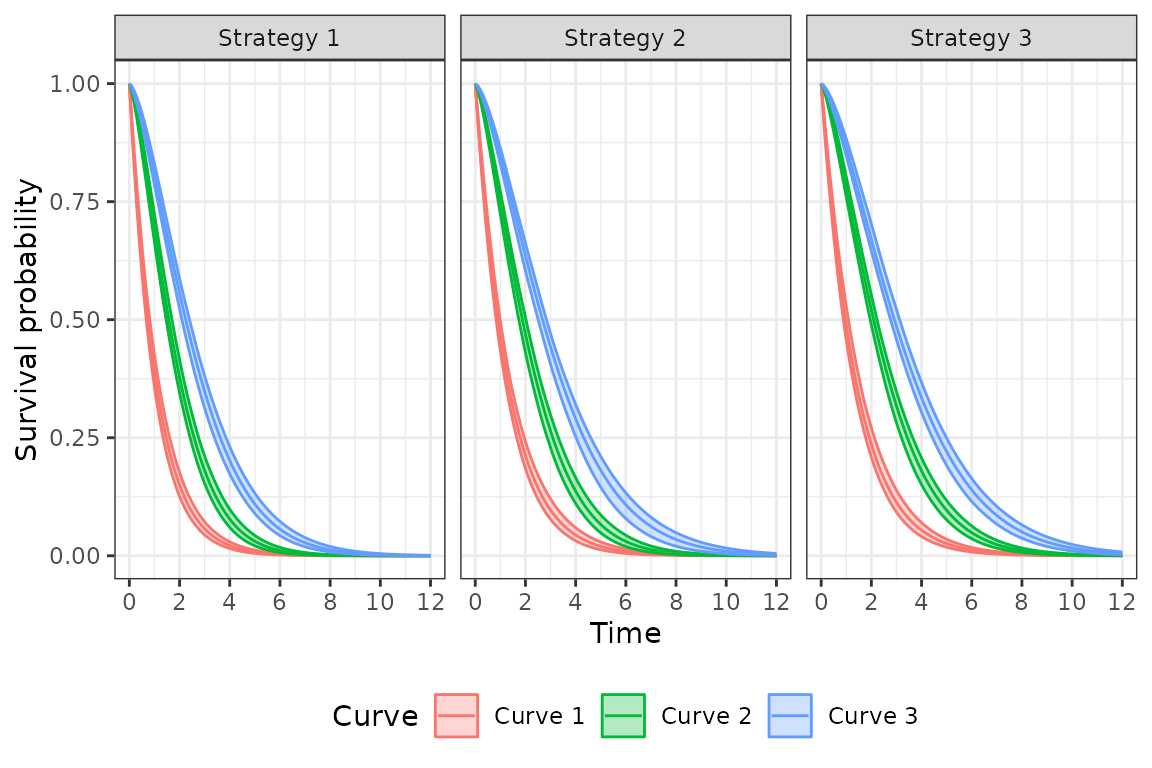

Simulating health state probabilities

After simulating survival, we can calculate the probability of being in each of the four health states using $sim_stateprobs(). At a given point in time, the probability of being in state 1 is the survival probability from the first survival curve, the probability of being in state 2 is the difference in survival probabilities between the 2nd and 1st curves, the probability of being in state 3 is the difference in survival probabilities between the 3rd and 2nd curves, and the probability of death is 1 minus the survival probability from curve 3.

While plots can be quickly generated with autoplot.stateprobs(), the output is returned in a tidy format (and stored as a field in the class named stateprobs_) that facilitates creation of custom plots. We’ll plot state probabilities for the 1st patient with the 30th randomly sampled parameter set.

# Simulate
psm$sim_stateprobs()
head(psm$stateprobs_)
##    sample strategy_id patient_id grp_id state_id     t      prob
##     <num>       <int>      <int>  <int>    <int> <num>     <num>
## 1:      1           1          1      1        1   0.0 1.0000000
## 2:      1           1          1      1        1   0.1 0.9189061
## 3:      1           1          1      1        1   0.2 0.8411512
## 4:      1           1          1      1        1   0.3 0.7688137
## 5:      1           1          1      1        1   0.4 0.7019982
## 6:      1           1          1      1        1   0.5 0.6405107
# Plot
stateprobs <- psm$stateprobs_[sample == 30 & patient_id == 1]
stateprobs[, state := factor(state_id, 
                             levels = rev(unique(state_id)))]
stateprobs[, strategy := factor(strategy_id, labels = names(labs$strategy_id))]
ggplot(stateprobs[strategy_id %in% c(1, 2, 3)],
            aes(x = t, y = prob, fill = state, group = state)) + 
  geom_area(alpha = .65) + facet_wrap(~strategy) +
  xlab("Years") + ylab("Proportion in state") +
  scale_fill_manual(name = "Health state",
                    values = c("gray92", "green4", "orange", "purple"),
                    labels = c("Death", 
                               rev(hesim_dat$states$state_name))) +
  scale_x_continuous(breaks = seq(0, max(times), 2)) +
  guides(fill = guide_legend(reverse = TRUE,
                             nrow = 2, byrow = TRUE)) + 
  theme(legend.position = "bottom")

Simulating costs and QALYs

Finally, we can simulate discounted costs and QALYs by numerically integrating the “weighted” probabilities in $stateprobs_ as described above. Costs and QALYs are produced for each treatment strategy, patient, health state, and sampled parameter set.

# Costs
psm$sim_costs(dr = .03)
head(psm$costs_)
##    sample strategy_id patient_id grp_id state_id    dr category    costs
##     <num>       <int>      <int>  <int>    <int> <num>   <char>    <num>
## 1:      1           1          1      1        1  0.03  medical 28707.06
## 2:      1           1          1      1        2  0.03  medical 24729.36
## 3:      1           1          1      1        3  0.03  medical 24914.92
## 4:      1           1          2      1        1  0.03  medical 27384.46
## 5:      1           1          2      1        2  0.03  medical 23700.48
## 6:      1           1          2      1        3  0.03  medical 23230.48
# QALYs
psm$sim_qalys(dr = .03)
head(psm$qalys_)
##    sample strategy_id patient_id grp_id state_id    dr     qalys       lys
##     <num>       <int>      <int>  <int>    <int> <num>     <num>     <num>
## 1:      1           1          1      1        1  0.03 0.8913423 1.0479377
## 2:      1           1          1      1        2  0.03 0.5448242 0.7391230
## 3:      1           1          1      1        3  0.03 0.5277850 0.7778092
## 4:      1           1          2      1        1  0.03 0.8502762 0.9996569
## 5:      1           1          2      1        2  0.03 0.5221563 0.7083712
## 6:      1           1          2      1        3  0.03 0.4921027 0.7252234

Decision analysis

A cost-effectiveness analysis can be performed with the cea() and cea_pw() functions after using the $summarize() method to create a hesim::ce object with mean costs and QALYs computed for each PSA sample. Details are provided in the cost-effectiveness analysis vignette.

ce_sim <- psm$summarize()
cea_out <- cea(ce_sim, dr_qalys = .03, dr_costs = .03)
cea_pw_out <- cea_pw(ce_sim, comparator = 1, dr_qalys = .03, dr_costs = .03)